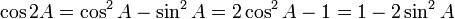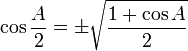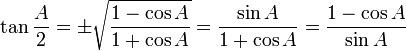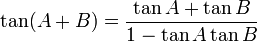Muhammad Rudiyansyah: November 2010

Kamis, 04 November 2010

Jawaban Soal Operasi Vektor

Secara singkat dapat dijelaskan bahwa :
Jarak adalah panjang lintasan yang ditempuh
Perpindahan adalah perubahan posisi suatu benda dari keadaan awal ke keadaan akhirnya

Contoh :

2. Gambar vektor dalam sistem koordinat Cartesian

3. Gambar dalam sistem koordinat Polar

4. Merubah vektor dalam koordinat Polar

5. Merubah vektor dalam koordinat Cartesian

6. Menghitung penambahan dan pengurangan operasi vektor

7. Menghitung perkalian titik (dot product)

8. Menghitung perkalian vektor (cross product)

Rabu, 03 November 2010

Vektor dalam matematika dan fisika adalah obyek geometri yang memiliki besar dan arah. Vektor jika digambar dilambangkan dengan tanda panah (→). Besar vektor proporsional dengan panjang panah dan arahnya bertepatan dengan arah panah. Vektor dapat melambangkan perpindahan dari titik A ke B. Vektor sering ditandai sebagai

$\overrightarrow{AB}.$

Vektor berperan penting dalam fisika: posisi, kecepatan dan percepatan obyek yang bergerak dan gaya dideskripsikan sebagai vektor.

Dari penjelasan tersebut di atas dapat diberikan contoh soal sebagai berikut :

Jawaban Soal

Sumber :

http://id.wikipedia.org/wiki/Vektor_%28spasial%29

Selasa, 02 November 2010

Geometri

1. Berapa nilai m pada segitiga siku-siku berikut menurut teorema Phytagoras :

2. Perhatikan gambar di bawah; jika P1(1,1), P2(3,3).

    Tentukan
    a. Koordinat titik T
    b. Jarak P1 - P2
    c. Jarak P1 - T
    d. Jarak P2 - T

      Diketahui :

x1 = 1 x2 = 3

y1 = 1 y2 = 3

a. Koordinat titik T

Jawab :

T = (x2 , y1)

T = (3 , 1)

b. Jarak P1 - P2

c. Jarak P1 - T

d. Jarak P2 - T

Cartesius

René Descartes lahir di La Haye, Perancis, 31 Maret 1596 – wafat di Stockholm, Swedia, 11 Februari 1650 pada umur 53 tahun), juga dikenal sebagai Renatus Cartesius dalam literatur berbahasa Latin, merupakan seorang filsuf dan matematikawan Perancis. Karyanya yang terpenting ialah Discours de la méthode(1637) dan Meditationes de prima Philosophia (1641).

Descartes, kadang dipanggil "Penemu Filsafat Modern" dan "Bapak Matematika Modern", adalah salah satu pemikir paling penting dan berpengaruh dalam sejarah barat modern. Dia menginspirasi generasi filsuf kontemporer dan setelahnya, membawa mereka untuk membentuk apa yang sekarang kita kenal sebagai rasionalisme kontinental, sebuah posisi filosofikal pada Eropa abad ke-17 dan 18.
Pemikirannya membuat sebuah revolusi falsafi di Eropa karena pendapatnya yang revolusioner bahwa semuanya tidak ada yang pasti, kecuali kenyataan bahwa seseorang bisa berpikir.
Dalam bahasa Latin kalimat ini adalah: cogito ergo sum sedangkan dalam bahasa Perancis adalah: Je pense donc je suis. Keduanya artinya adalah:
"Aku berpikir maka aku ada". (Inggris: I think, therefore I am)
Meski paling dikenal karena karya-karya filosofinya, dia juga telah terkenal sebagai pencipta sistem koordinat Kartesius, yang mempengaruhi perkembangan kalkulus modern.

(Sumber: http://id.wikipedia.org/wiki/Rene_Descartes)

Trigonometri

Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu. Matematikawan India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri. Lagadha adalah matematikawan yang dikenal sampai sekarang yang menggunakan geometri dan trigonometri untuk penghitungan astronomi dalam bukunya Vedanga, Jyotisha, yang sebagian besar hasil kerjanya hancur oleh penjajah India.

Matematikawan Yunani Hipparchus sekitar 150 SM menyusun tabel trigonometri untuk menyelesaikan segi tiga.

Matematikawan Yunani lainnya, Ptolemy sekitar tahun 100 mengembangkan penghitungan trigonometri lebih lanjut.

Matematikawan Silesia Bartholemaeus Pitiskus menerbitkan sebuah karya yang berpengaruh tentang trigonometri pada 1595 dan memperkenalkan kata ini ke dalam bahasa Inggris dan Perancis.

Dari soal Quiz matematika dapat dijabarkan sebagai berikut :

Hubungan Fungsi Trigonometri

$\sin^2 A + \cos^2 A = 1 \,$

$1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,$

$1 + \cot^2 A = \csc^2 A \,$

$\tan A = \frac{\sin A}{\cos A}\,$

Penjumlahan

$\sin (A + B) = \sin A \cos B + \cos A \sin B \,$

$\sin (A - B) = \sin A \cos B - \cos A \sin B \,$

$\cos (A + B) = \cos A \cos B - \sin A \sin B \,$

$\cos (A - B) = \cos A \cos B + \sin A \sin B \,$

Rumus sudut rangkap dua

$\sin 2A = 2 \sin A \cos A \,$

$\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,$

$\tan 2A = {2 \tan A \over 1 - \tan^2 A} = {2 \cot A \over \cot^2 A - 1} = {2 \over \cot A - \tan A} \,$

Rumus sudut rangkap tiga

$\sin 3A = 3 \sin A - 4 \sin^3 A \,$

$\cos 3A = 4 \cos^3 A - 3 \cos A \,$

Rumus setengah sudut

$\sin \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{2}} \,$

$\cos \frac{A}{2} = \pm \sqrt{\frac{1+\cos A}{2}} \,$

$\tan \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} \,$

$\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \,$

Titik dan Garis

Dari judul tersebut dapat diberikan contoh soal-soal serta jawaban tentang titik dan garis.
1. Carilah 5 titik yang dilalui garis 3x - 2y = 8. Gambarkan pada sistem koordinat Cartesian

2. Buatlah fungsi garis y = f(x) yang lelaui titik (1,0) dan (-3,3) dan carilah nilai kemiringannya (slope)

3. Di titik mana kemungkinan terjadinya tabrakan antara mobil yang bergerak pada jalur garis no.2 dan pada
jalur garis -x + 3y = -6
Jawab :

Sejarah Phytagoras

Phytagoras lahir pada tahun 570 SM, di pulau Samos, di daerah Ionia. Pythagoras (582 SM – 496 SM, bahasa Yunani: Πυθαγόρας) adalah seorang matematikawan dan filsuf Yunani yang paling dikenal melalui teoremanya.Dikenal sebagai “Bapak Bilangan”, dia memberikan sumbangan yang penting terhadap filsafat dan ajaran keagamaan pada akhir abad ke-6 SM. Kehidupan dan ajarannya tidak begitu jelas akibat banyaknya legenda dan kisah-kisah buatan mengenai dirinya.

Dalam tradisi Yunani, diceritakan bahwa ia banyak melakukan perjalanan, diantaranya ke Mesir. Perjalanan Phytagoras ke Mesir merupakan salah satu bentuk usahanya untuk berguru, menimba ilmu, pada imam-imam di Mesir. Konon, karena kecerdasannya yang luar biasa, para imam yang dikunjunginya merasa tidak sanggup untuk menerima Phytagoras sebagai murid. Namun, pada akhirnya ia diterima sebagai murid oleh para imam di Thebe. Disini ia belajar berbagai macam misteri. Selain itu, Phytagoras juga berguru pada imam-imam Caldei untuk belajar Astronomi, pada para imam Phoenesia untuk belajar Logistik dan Geometri, pada para Magi untuk belajar ritus-ritus mistik, dan dalam perjumpaannya dengan Zarathustra, ia belajar teori perlawanan.

Selepas berkelana untuk mencari ilmu, Phytagoras kembali ke Samos dan meneruskan pencarian filsafatnya serta menjadi guru untuk anak Polycartes, penguasa tiran di Samos. Kira-kira pada tahun 530, karena tidak setuju dengan pemerintahan tyrannos Polycartes, ia berpindah ke kota Kroton di Italia Selatan. Di kota ini, Phytagoras mendirikan sebuah tarekat beragama yang kemudian dikenal dengan sebutan “Kaum Phytagorean.”

Kaum phytagorean sangat berjasa dalam meneruskan pemikiran-pemikiran Phytagoras. Semboyan mereka yang terkenal adalah “authos epha, ipse dixit” (dia sendiri yang telah mengatakan demikian).2 Kaum ini diorganisir menurut aturan-aturan hidup bersama, dan setiap orang wajib menaatinya. Mereka menganggap filsafat dan ilmu pengetahuan sebagai jalan hidup, sarana supaya setiap orang menjadi tahir, sehingga luput dari perpindahan jiwa terus-menerus.
Diantara pengikut-pengikut Phytagoras di kemudian hari berkembang dua aliran. Yang pertama disebut akusmatikoi (akusma = apa yang telah didengar; peraturan): mereka mengindahkan penyucian dengan menaati semua peraturan secara seksama. Yang kedua disebut mathematikoi (mathesis = ilmu pengetahuan): mereka mengutamakan ilmu pengetahuan, khususnya ilmu pasti.

Pemikiran Phytagoras

Phytagoras percaya bahwa angka bukan unsur seperti udara dan air yang banyak dipercaya sebagai unsur semua benda. Angka bukan anasir alam. Pada dasarnya kaum Phytagorean menganggap bahwa pandangan Anaximandros tentang to Apeiron dekat juga dengan pandangan Phytagoras. To Apeiron melepaskan unsur-unsur berlawanan agar terjadi keseimbangan atau keadilan (dikhe). Pandangan Phytagoras mengungkapkan bahwa harmoni terjadi berkat angka. Bila segala hal adalah angka, maka hal ini tidak saja berarti bahwa segalanya bisa dihitung, dinilai dan diukur dengan angka dalam hubungan yang proporsional dan teratur, melainkan berkat angka-angka itu segala sesuatu menjadi harmonis, seimbang. Dengan kata lain tata tertib terjadi melalui angka-angka.

Salah satu peninggalan Phytagoras yang terkenal adalah teorema Pythagoras, yang menyatakan bahwa kuadrat hipotenusa dari suatu segitiga siku-siku adalah sama dengan jumlah kuadrat dari kaki-kakinya (sisi-sisi siku-sikunya). Walaupun fakta di dalam teorema ini telah banyak diketahui sebelum lahirnya Pythagoras, namun teorema ini dikreditkan kepada Pythagoras karena ia lah yang pertama membuktikan pengamatan ini secara matematis.[1]

Pythagoras dan murid-muridnya percaya bahwa segala sesuatu di dunia ini berhubungan dengan matematika, dan merasa bahwa segalanya dapat diprediksikan dan diukur dalam siklus beritme. Ia percaya keindahan matematika disebabkan segala fenomena alam dapat dinyatakan dalam bilangan-bilangan atau perbandingan bilangan. Ketika muridnya Hippasus menemukan bahwa sqrt{2}, hipotenusa dari segitiga siku-siku sama kaki dengan sisi siku-siku masing-masing 1, adalah bilangan irasional, Pythagoras memutuskan untuk membunuhnya karena tidak dapat membantah bukti yang diajukan Hippasus

Sumber :

http://id.wikipedia.org/wiki/Pythagoras